WARNING: The 2.x versions of Elasticsearch have passed their EOL dates. If you are running a 2.x version, we strongly advise you to upgrade.
This documentation is no longer maintained and may be removed. For the latest information, see the current Elasticsearch documentation.
Theory Behind Relevance Scoring
editTheory Behind Relevance Scoring
editLucene (and thus Elasticsearch) uses the Boolean model to find matching documents, and a formula called the practical scoring function to calculate relevance. This formula borrows concepts from term frequency/inverse document frequency and the vector space model but adds more-modern features like a coordination factor, field length normalization, and term or query clause boosting.
Don’t be alarmed! These concepts are not as complicated as the names make them appear. While this section mentions algorithms, formulae, and mathematical models, it is intended for consumption by mere humans. Understanding the algorithms themselves is not as important as understanding the factors that influence the outcome.
Boolean Model
editThe Boolean model simply applies the AND, OR, and NOT conditions
expressed in the query to find all the documents that match. A query for
full AND text AND search AND (elasticsearch OR lucene)
will include only documents that contain all of the terms full, text, and
search, and either elasticsearch or lucene.
This process is simple and fast. It is used to exclude any documents that cannot possibly match the query.
Term Frequency/Inverse Document Frequency (TF/IDF)
editOnce we have a list of matching documents, they need to be ranked by relevance. Not all documents will contain all the terms, and some terms are more important than others. The relevance score of the whole document depends (in part) on the weight of each query term that appears in that document.
The weight of a term is determined by three factors, which we already introduced in What Is Relevance?. The formulae are included for interest’s sake, but you are not required to remember them.
Term frequency
editHow often does the term appear in this document? The more often, the higher the weight. A field containing five mentions of the same term is more likely to be relevant than a field containing just one mention. The term frequency is calculated as follows:
tf(t in d) = √frequency
|
The term frequency ( |
If you don’t care about how often a term appears in a field, and all you care about is that the term is present, then you can disable term frequencies in the field mapping:
Inverse document frequency
editHow often does the term appear in all documents in the collection? The more
often, the lower the weight. Common terms like and or the contribute
little to relevance, as they appear in most documents, while uncommon terms
like elastic or hippopotamus help us zoom in on the most interesting
documents. The inverse document frequency is calculated as follows:
idf(t) = 1 + log ( numDocs / (docFreq + 1))
Field-length norm
editHow long is the field? The shorter the field, the higher the weight. If a
term appears in a short field, such as a title field, it is more likely that
the content of that field is about the term than if the same term appears
in a much bigger body field. The field length norm is calculated as follows:
norm(d) = 1 / √numTerms
While the field-length norm is important for full-text search, many other
fields don’t need norms. Norms consume approximately 1 byte per string field
per document in the index, whether or not a document contains the field. Exact-value not_analyzed string fields have norms disabled by default,
but you can use the field mapping to disable norms on analyzed fields as
well:
PUT /my_index
{
"mappings": {
"doc": {
"properties": {
"text": {
"type": "string",
"norms": { "enabled": false }
}
}
}
}
}
|
This field will not take the field-length norm into account. A long field and a short field will be scored as if they were the same length. |
For use cases such as logging, norms are not useful. All you care about is whether a field contains a particular error code or a particular browser identifier. The length of the field does not affect the outcome. Disabling norms can save a significant amount of memory.
Putting it together
editThese three factors—term frequency, inverse document frequency, and field-length norm—are calculated and stored at index time. Together, they are used to calculate the weight of a single term in a particular document.
When we refer to documents in the preceding formulae, we are actually talking about a field within a document. Each field has its own inverted index and thus, for TF/IDF purposes, the value of the field is the value of the document.
When we run a simple term query with explain set to true (see
Understanding the Score), you will see that the only factors involved in calculating the
score are the ones explained in the preceding sections:
PUT /my_index/doc/1
{ "text" : "quick brown fox" }
GET /my_index/doc/_search?explain
{
"query": {
"term": {
"text": "fox"
}
}
}
The (abbreviated) explanation from the preceding request is as follows:
weight(text:fox in 0) [PerFieldSimilarity]: 0.15342641 result of: fieldWeight in 0 0.15342641 product of: tf(freq=1.0), with freq of 1: 1.0 idf(docFreq=1, maxDocs=1): 0.30685282 fieldNorm(doc=0): 0.5
|
The final |
|
|
The term |
|
|
The inverse document frequency of |
|
|
The field-length normalization factor for this field. |
Of course, queries usually consist of more than one term, so we need a way of combining the weights of multiple terms. For this, we turn to the vector space model.
Vector Space Model
editThe vector space model provides a way of comparing a multiterm query against a document. The output is a single score that represents how well the document matches the query. In order to do this, the model represents both the document and the query as vectors.
A vector is really just a one-dimensional array containing numbers, for example:
[1,2,5,22,3,8]
In the vector space model, each number in the vector is the weight of a term, as calculated with term frequency/inverse document frequency.
While TF/IDF is the default way of calculating term weights for the vector space model, it is not the only way. Other models like Okapi-BM25 exist and are available in Elasticsearch. TF/IDF is the default because it is a simple, efficient algorithm that produces high-quality search results and has stood the test of time.
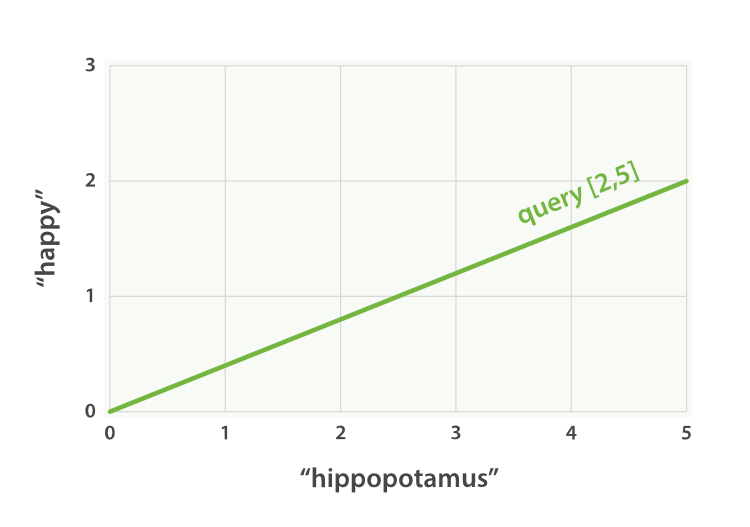
Imagine that we have a query for “happy hippopotamus.” A common word like
happy will have a low weight, while an uncommon term like hippopotamus
will have a high weight. Let’s assume that happy has a weight of 2 and
hippopotamus has a weight of 5. We can plot this simple two-dimensional
vector—[2,5]—as a line on a graph starting at point (0,0) and
ending at point (2,5), as shown in Figure 27, “A two-dimensional query vector for “happy hippopotamus” represented”.
Now, imagine we have three documents:
- I am happy in summer.
- After Christmas I’m a hippopotamus.
- The happy hippopotamus helped Harry.
We can create a similar vector for each document, consisting of the weight of
each query term—happy and hippopotamus—that appears in the
document, and plot these vectors on the same graph, as shown in Figure 28, “Query and document vectors for “happy hippopotamus””:
-
Document 1:
(happy,____________)—[2,0] -
Document 2:
( ___ ,hippopotamus)—[0,5] -
Document 3:
(happy,hippopotamus)—[2,5]
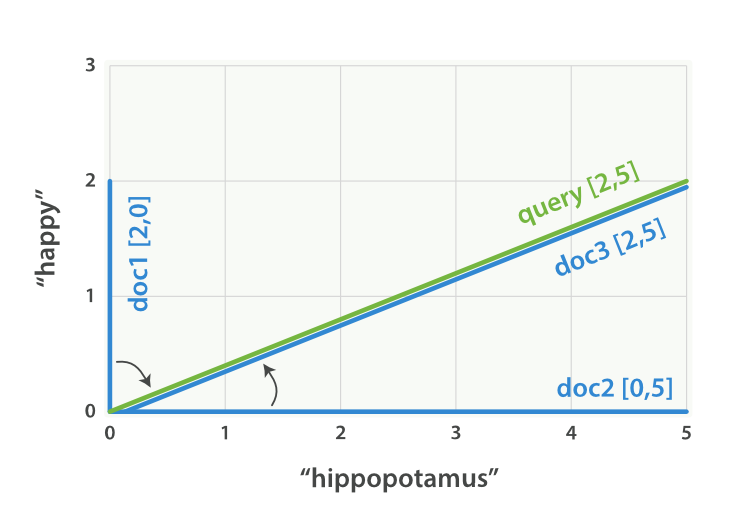
The nice thing about vectors is that they can be compared. By measuring the angle between the query vector and the document vector, it is possible to assign a relevance score to each document. The angle between document 1 and the query is large, so it is of low relevance. Document 2 is closer to the query, meaning that it is reasonably relevant, and document 3 is a perfect match.
In practice, only two-dimensional vectors (queries with two terms) can be plotted easily on a graph. Fortunately, linear algebra—the branch of mathematics that deals with vectors—provides tools to compare the angle between multidimensional vectors, which means that we can apply the same principles explained above to queries that consist of many terms.
You can read more about how to compare two vectors by using cosine similarity.
Now that we have talked about the theoretical basis of scoring, we can move on to see how scoring is implemented in Lucene.